[컴퓨터구조] 3강. 디지털 논리 회로
디지털 논리 회로
논리 회로
논리회로란?
- 전기적 신호를 이용하여 (off: 0, on: 1) 자료를 정보로 가공할 수 있도록 제작된 기계
- 디지털 코드로 정의한 특정 대상을 처리하기 위해 전기적 신호를 제어하는 회로가 필요하고, 이를 위해 제작된 회로
Gate
- 0, 1의
이진 정보를 처리하는 논리회로 - 여러 종류가 존재
- 동작은
부울 대수 이용해 표현 - 입려과 출력의 관계는
진리표로 표시
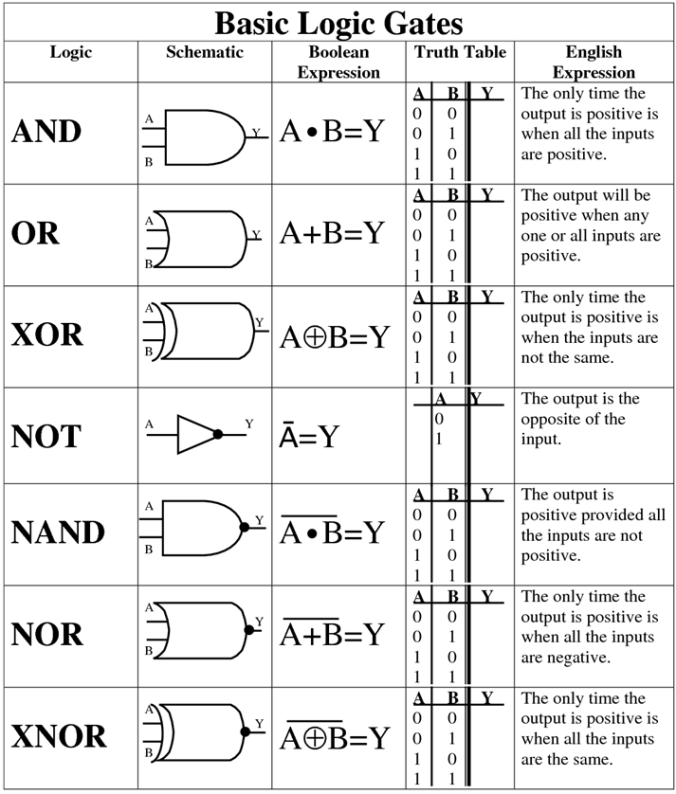
| 게이트 종류 | 역할 | 논리식 |
|---|---|---|
| AND 게이트 | 곱하기 | X = A * B |
| OR 게이트 | 더하기 | X = A + B |
| NOT 게이트 | 반대 | X = !A |
| XOR 게이트 | 베타적 논리합 : 두 결과가 다를때는 true, 같으면 false | X = A (+) B |
| NAND 게이트 | 곱하기 한 결과의 반대 | X = !(A * B) |
| NOR 게이트 | 더하기 한 결과의 반대 | X = !(A + B) |
| E-NOR 게이트 | 베타적 논리합 : 두 결과가 다를때는 true, 같으면 false 의 반대 | X = !(A (+) B) |
유니버셜 게이트
- NAND와 NOR 게이트
- 모든 게이트의 구성 가능
- NAND 게이트를 사용한 AND 게이트 구성 가능
- NOR 게이트를 사용한 AND 게이트 구성 가능
부울 대수
- 2진 변수와 논리동작을 취급하는 대수
- 논리회로의 형태와 구조를 기술하는데 필요한 수학적인 이론
- f = x +(or) y’(not) *(and) z
- 변수 사이의 진리표 관계를 대수형식으로 표현
- 논리도의 입출력 관계를 대수형식으로 표시
- 동일한 성능을 갖는 더 간단한 회로를 만들기에 편리
| 순서 | 관계 |
|---|---|
| 1 | X + 0 = X |
| 2 | X * 0 = 0 |
| 3 | X + 1 = X |
| 4 | X * 1 = X |
| 5 | X + X = X |
| 6 | X * X = X |
| 7 | X + X’ = 1 |
| 8 | X * X’ = 0 |
| 9 | X + Y = Y + X |
| 10 | XY = YX |
| 11 | X + (Y+Z) = (X+Y) + Z |
| 12 | X(YZ) = (XY)Z |
| 13 | X(Y+Z) = XY + XZ |
| 14 | X + YZ = (X+Y)(X+Z) |
| 15 | (X + Y)’ = X’Y’ |
| 16 | (XY)’ = X’ + Y’ |
| 17 | (X’)’ = X |
교환 법칙 : 단순 곱하기와 덧셈은 요소의 순서를 교환해도 값이 같다.
- A * B = B * A
- A + B = B + A
결합 법칙 : 곱하기와 더하기로 순수하게 이루어진 것은 어느 곳에 괄호를 쳐도 같다.
- A * (B * C) = (A * B) * C
- (A + B) + C = A + (B + C)
분배 법칙 : 합의 곱은 합의 요소에 곱한 것과 같다.
- A * (B + C) = A * B + A * C
다중부정 : 부정의 부정은 긍정이다.
- A’’ = A
드모르강(Demorgan) 법칙
- NOR와 NAND를 취급하는데 유용
- (A + B)’ = A’ * B’
카르노 도표 : 카르노 맵(Karnaugh map)을 이용한 부울 함수 간소화
- 부울 대수식을 간소화하기 위한 가장 체계적이고, 간단한 방법
- 최적의 간략화에 근거한 디지털 회로설계만이 게이트 수의 최소화 가능
- 회로의 경제성, 회로의 신뢰성, 소비전력의 효율성, 제품의 소형화 가능
- 맨 앞자리수가 row, 나머지를 column으로 잡아서 맵 작성